A Game as Hard as Integer Factorization
Anyone who still remembers the elementary school method of multiplying two integers should agree that this problem is easy even when armed only with pen and paper. Calculating 167714 x 988675 might look cumbersome at a first sight but, if you have to do it, it will take you few minutes or so. What about multiplying 65446568786432344 x 1976544568? This is probably twice as annoying and time consuming compared to the previous multiplication, however, it is still do-able in a reasonable amount of time.
What about the reverse problem, the so called integer factorization problem?
That is, how easy is it to find two numbers (factors)
RSA-232 = 100988139787192354690956489430946858281823382195557395514112051620583102
133852854537436610975715436366491338008491706516992170152473329438927028
023438096090980497644054071120196541074755382494867277137407501157718230
5398340606162079
There is currently the belief that, for even slightly bigger numbers as RSA-1024, only a quantum computer can find the factors in a reasonable time.
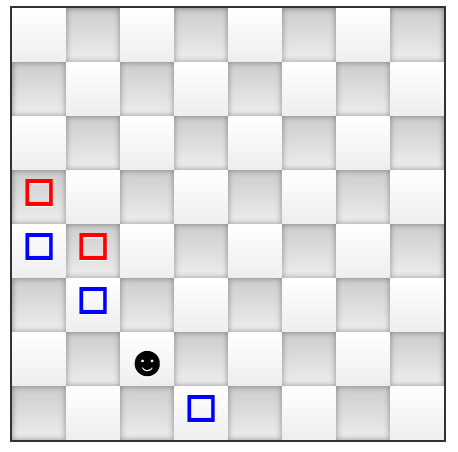
People usually don't like solving number related problems, but they spend time easily on board games, even if these games are hard. Can integer factorization be seen as a board game? It turns out that yes, you can reduce any integer factorization problem to a solitaire game played with tokens on a big enough chess board. To explain the rules let's start with a normal chess board having only one token at position C2. There are only two kinds of moves: either moving the token on the top-left down-right diagonal (the "blue" moves), or replacing the token with two new tokens located on the next (top-left down-right) diagonal.
For example a "blue" move could be moving the token from C2 to D1 as shown in the following image:
 ⇒
⇒
while a "red" move is replacing the token from C2 with two tokens located on the E1-A5 diagonal, as shown in the image that follows.
 ⇒
⇒

When would this game end? We call it a win whenever the tokens are positioned in a column and rows pattern. For example, the following images show two different game ending positions:


Before pondering and finding yourself why is this game as hard as integer factorization why don't you give it a try and play the integer factorization game now?
(Go here for an explanation on why this game is hard.)